| SKYLINES & SCRAPERS HOME | THE WORLD'S BEST SKYLINES | THE WORLD'S TALLEST BUILDINGS | ONE CENTURY OF SKYSCRAPERS | SKYSCRAPER HEIGHTS ANALYSIS | THE MATHEMATICAL CITY | LINKS | FEEDBACK |
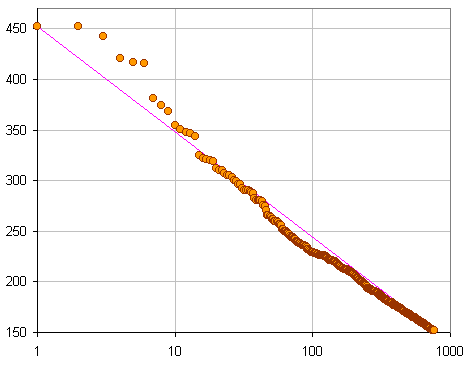
Vertical axis: height in meters,
horizontal axis: number of buildings with at least this height
Based on Marshall's Hot 500, july 1999.

 |
created: 1999-07-23 last update: 2002-02-20 |